JAVA - Tập 2 | Data Structures và Algorithms | Tổng Quan
- Apr 17, 2020
- 9 min read
Updated: Apr 19, 2020
Before reading:
Bài viết được tham khảo dựa vào bài viết của tác giả Jeff Friesen, đăng ngày 10/8/2017 trên một trang web lớn dành cho cộng đồng lập trình viên JAVA là JAVAWORLD.
Link bài viết tại đây.
Lời nói đầu
Những lập trình viên Java thường sử dụng Data Structures để có thể lưu và tổ chức dữ liệu, đồng thời xài Algorithms để có thể sử dụng hiệu quả các Data đó cho mục đích riêng của họ. Có một điều không thể chối cãi khi mà khẳng định rằng: "Càng nắm rõ bản chất của Data Structures và Algorithms thì khi làm việc cùng nhau, các lập trình viên lại cho ra đời những chương trình JAVA hoạt động trơn tru và hiệu quả"
Nội dung bài viết này sẽ gồm 4 phần như sau:
Data Structure là gì ?
Các loại Data Structure
Mẫu thiết kế (Design Pattern) và Data Structures
Algorithm là gì ?
Lưu đồ và mã giả
1. Data Structure là gì ?
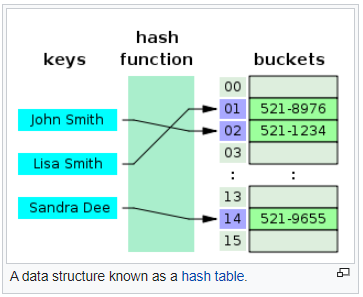
Trong nghành khoa học máy tình, Data Structure được hiểu chính là nơi dữ liệu được lưu trữ, tổ chức và quản lý. Cấu trúc của nơi lưu trữ ấy được thiết kế sao cho có thể cho phép lấy dữ liệu ra và đưa dữ liệu vào một cách trơn tru có hiệu quả
Vậy để có thể thiết kế được một nơi như vậy, đòi hỏi có một cơ sở cho nó. Data Structures được dựa trên một khái niệm có tên là "Kiểu dữ liệu trừu tượng - Abstract data types (ADT)". Một kiểu dữ liệu trừu tượng là một mô hình toán học cùng với một tập hợp các phép toán trên nó. Có thể hiểu kiểu dữ liệu trừu tượng chính là một kiểu dữ liệu do chính chúng ta định nghĩa ở mức khái niệm ( Conceptual ), nó chưa được cài đặt cụ thể bằng một ngôn ngữ lập trình.
Khi muốn cài đặt một kiểu dữ liệu trừu tượng trên một ngôn ngữ lập trình cụ thể, ta phải thực hiện 2 nhiệm vụ sau:
Biểu diễn kiểu dữ liệu trừu tượng bằng một cấu trúc dữ liệu hoặc một kiểu dữ liệu trừu tượng khác đã được cài đặt trước.
Viết các chương trình con thực hiện các phép toán trên kiểu dữ liệu trừu tượng mà ta thường gọi là cài đặt các phép toán.
Ví dụ về ADT rõ nhất đó chính là List. List được xem như là một nơi chứa các thành phần (Elements). Mỗi thành phần trong List thì có một vị trí riêng và List cho phép trung lặp giá trị giữa các thành phần. Các phép toán cơ bản trên một List thông thường như sau:
Tạo mới 1 List
Thêm một giá trị mới vào cuối List đó
Chèn một giá trị vào List
Xóa một giá trị khỏi List
Duyệt qua List
Xóa List
Data structure có thể thực thì List ADT thông qua các việc như thay đổi kích thước của List, đưa về mảng một chiều hoặc một danh sách liên kết đơn các giá trị có trong List đó.
2. Các loại Data Structure
Có rất nhiều loại Data Structure, trải dài từ một biến(Variables) đứng riêng lẻ cho đến một Array hay Linked List chưa các đối tượng mà có nhiều Fields trong đó. Ví dụ: 1 mảng danh sách các sinh viên, mỗi sinh viên thì chứa mã số sinh viên, điểm số, quê quán, trường học ...
Nói tóm lại, thì chủ yếu có tất cả 3 loại chính: Primitives, Aggregates, Container. Nói về khái niệm sẽ rất là phức tạp nên mình chỉ đưa ra ví dụ là các bạn nhìn phát là biết ngay (dân chơi).
Primitives: Các biến mà dùng để lưu các giá trị int, float, long, boolean ...
Aggregates: Lưu được nhiều dữ liệu, nhiều trường như Array, Object ...
Conatiner: Tương tự khái niệm Structure trong C++ như Employee, Vehicle...
3. Mẫu thiết kế (Design Pattern) và Data Structures
Việc sử dụng các Design Pattern để giới thiệu cho sinh viên đại học biết về Data Structure là khá phổ biến. Một nghiên cứu của trường đại học Brown University cho thấy rằng khi sử dụng Design Patterns giúp tạo ra các Data Structures có "chất lượng cao - high quality".
Ví dụ dưới đây cho thấy việc sử dụng Adapter Pattern dành cho việc thiết kế ra các Stacks và Queues.
public class DequeStack implements Stack
{
Deque D; // holds the elements of the stack
public DequeStack()
{
D = new MyDeque();
}
@Override
public int size()
{
return D.size();
}
@Override
public boolean isEmpty()
{
return D.isEmpty();
}
@Override
public void push(Object obj)
{
D.insertLast(obj);
}
@Override
public Object top() throws StackEmptyException
{
try
{
return D.lastElement();
}
catch(DequeEmptyException err)
{
throw new StackEmptyException();
}
}
@Override
public Object pop() throws StackEmptyException
{
try
{
return D.removeLast();
}
catch(DequeEmptyException err)
{
throw new StackEmptyException();
}
}
}4. Algorithm là gì ?
Theo dòng lịch sử thì đã cho thấy các nhà khoa học đã từng tìm kiếm và sử dùng nhiều công cụ để giúp cho việc tính toán toán học, công cụ ở đây có thể hiểu rộng hơn là máy tính tay hay máy tính bàn mà còn là các mô hình, nguyên lý, định lý toán học. Trong tất cả các công cụ đó thì thuật toán Algorithm là công cụ được sử dụng mà có tính tương thích, kết nối sâu nhất với ngành Khoa học Máy tính - Computer Sience.
Theo định nghĩa thì Thuật toán chính là một chuỗi các hướng dẫn giúp hoàn thành một tác vụ, một công việc trong một khoảng thời gian xác định. Một thuật toán thì thường tuân thủ các quy định sau:
Nhận không hoặc nhiều giá trị đầu vào Input.
Trả về ít nhất một giá trị đầu ra Output
Các thuật toán được hình thành từ những hướng dẫn - Instruction rõ ràng, không mơ hồ
Có kết thúc sau khi chạy hữu hạn các bước
Thuật toán không cần phải quá cao siêu, nó có thể cho người tìm hiểu phác thảo trên giấy
Chú ý rằng trong quá trình chạy thuật toán thì nhiều chương trình sẽ không tự kết thúc nếu không có sự tác động, can thiệp từ bên ngoài.
Xây dựng một thuật toán được thực hiện dựa trên một chuỗi các dòng code. Một ví dụ đó là khi bạn có một chương trình bao gồm chuỗi các dòng lệnh mà công việc cuối cùng của nó chính là để in một báo cáo, như vậy ta vẫn có thể xem đó là một ví dụ cho việc sử dụng thuật toán để thực thi một công việc. Một ví dụ nữa và khá nỗi tiếng đó là thuật toán Euclid. Thuật toán này được áp dụng trong việc tìm ước số chung lớn nhất trong toán học.
5. Lưu đồ và mã giả
Lưu đồ chính là mô hình hóa một cách trực quan việc chạy một thuật toán như thế nào, gồm những bước nào, chạy ra làm sao (Algorithm's Control Flow). Việc lập tức viết code mà nắm vững được các luồng điều khiển của thuật toán sẽ dẫn đến việc sinh ra nhiều Bugs trong quá trình kiểm thử chương trình. Lưu đồ và mã giả sinh ra để giải quyết các vấn đề đó.
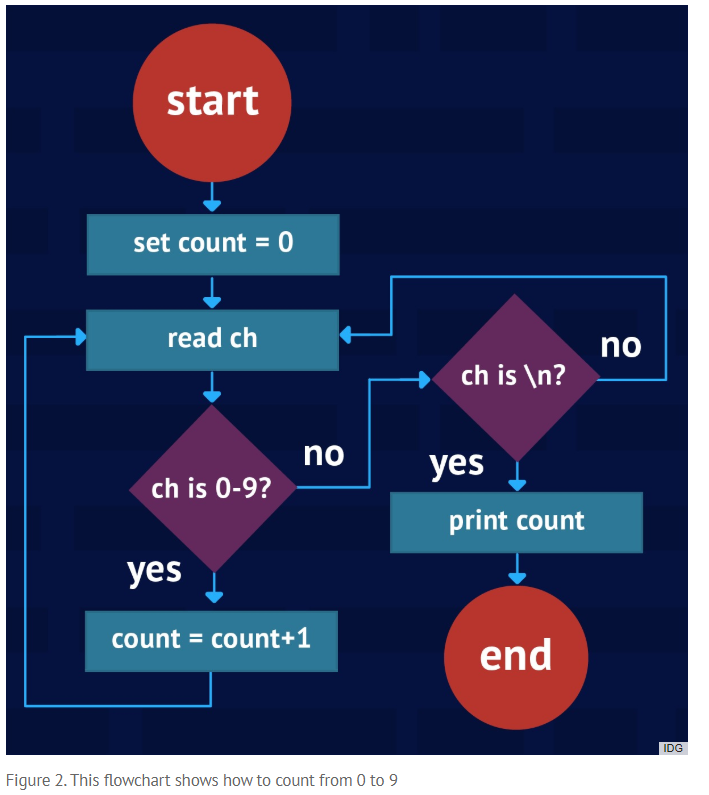
Hình trên giải thích ý nghĩa của các thành phần trong một lưu đồ:
Hình chữ nhật: Trạng thái, nơi bạn khai báo biến, xử lý tính toán, xuất giá trị..
Dấu mũi tên: Luồng xử lý
Hình thoi: Đưa ra điều kiện, hoặc lựa chọn cần kiểm tra
Hình tròn: Đầu vào hoặc kết thúc lưu đồ
Ví dụ:
Đề bài: Xây dựng một lưu đồ chương trình đọc các kí tự trong một chuỗi, nếu phát hiện kí tự là số thì tăng biến đếm, còn là khác kí tự số thì in nó ra cho đến khi hết chuỗi đó thì in kết quả biến đếm cuối cùng ?
Trả lời: Lưu đồ như sau:
Tương tự cho bài toán trên, chúng ta có mã giả như sau:
DECLARE CHARACTER ch = ''
DECLARE INTEGER count = 0
DO
READ ch
IF ch GE '0' AND ch LE '9' THEN
count = count + 1
END IF
UNTIL ch EQ '\n'
PRINT count
ENDBonus kiến thức
+ Chọn đúng thuật toán
Có một sự thật mà ít người để ý đó chính là khi chúng ta lựa chọn Data Structures và Algorithms để sử dụng thì ứng dụng sẽ bị tác động 2 mặt như sau:
Memory Usage (Việc sử dụng bộ nhớ như thế nào khi lựa chọn kiểu processđó )
CPU time (Thời gian CPU thức thi, việc này chủ yếu bị Algorithms tác động tương ứng vs các Data Structures đã khai báo ở trên )
+ Cân bằng giữa Memory và CPU
Giữa Memory Usage và CPU có một mối quan hệ ngược với nhau như sau: Khi bạn sử dụng ít dung lượng bộ nhớ cho Data Structures thì CPU sẽ tốn nhiều thời gian hơn cho "xử lý" những Data Items có trong Data Structures và ngược lại.
Do đó khi code chúng ta cầnn cố gắng sao cho cân bằng được giữa Data Structures và CPU time. Lựa chọn việc sử dụng thuật toán nào, ở đâu bằng cách so sánh, chạy thử sẽ là một phương pháp tốt để giả quyết chuyện này.
Độ phức tạp của thuật toán
Độ phức tạp của thuật toán Time Complexity (TM) được định nghĩa là "Tổng thời gian cần thiết để một thuật toán có thể thực thi xong". Để tính độ phức tạp thì thế giới đã định nghĩa ra 3 phương pháp như sau:
Big Oh (O): Code mà chưa được tối ưu, rơi vào case tệ nhất, có thời gian thực thi lâu nhất
Big Omega (Ω): Rút kinh nghiệm, code được tối ưu nhất có thể, nên rơi vào case tốt nhất, có thời gian thực thi nhanh nhất.
Big Theta (Θ): Bao gồm cả trường hợp tệ nhất và tốt nhất
Theo như mình tìm hiểu thì phương pháp thứ 1 Big Oh là phương pháp thông dụng nhất để tính và được dạy nhiều trong môi trường giáo dục và ngày cả đi làm sau này. Big Oh được chia làm rất nhiều trường hợp và 3 trường hợp phổ biến nhất là O(n), O(logn), O(n²). Giải thích cho 3 ví dụ này thì mình kiếm được một ví dụ rất dễ hiểu trên trang Medium như sau:
" Bạn ra phố đi bộ Nguyễn Huệ tìm gấu vì bạn đang ế chảy thây ra. Vậy tìm bằng cách nào đây:
Giả sử (n) là tổng số người mà bạn sẽ tương tác ở phố đi bộ
O(n): nếu bạn đi hỏi từng người “Tui đang rảnh, bạn yêu tui cho tui bớt rảnh lại chút được hơm?”, đến khi tìm thấy ai đó say Yes → xong Nghĩa là: Nếu số nhọ thì bạn phải hỏi hết (n) người thì có thể tìm được gấu (hoặc cũng có thể không tìm được luôn)
O(logn): nếu bạn nói “Ai có khả năng rảnh để yêu tui thì đứng lại đây, còn không thì lui xuống hậu cung dùm”, vậy là đã giảm đi phân nửa thành phần phản động (và cũng có khả năng giải quyết luôn bài toán vì không còn ai ở lại =)) ). Với những người còn lại, tiếp tục hỏi câu hỏi trên…đến khi không còn 1 ai… à, đến khi tìm được người cuối cùng chịu làm gấu của bạn → xong Nghĩa là: cứ mỗi lần bạn đặt câu hỏi thì sẽ giảm đc 1/2 số lượng người. Nếu n = 10 thì xui lắm hỏi 5 lần là xong
O(n²): nếu bạn túm 1 người đi đường A và hỏi “Thím, yêu tui nha?”, nếu A nói không, 2 người ngồi xuống đàm đạo, bạn hỏi ý kiến của A về (n-1) người còn lại, xem họ có yêu bạn không… và bạn cứ đi hỏi rồi ngồi đàm đạo… đến khi xuống lỗ thì thôi → xong Nghĩa là: cứ gặp 1 người bạn phải hỏi (n) lần (1 lần hỏi người đó, và n-1 lần hỏi người đó những người còn lại) "
Link ví dụ tại đây
Các quy tắc tính TM
Để tính TM thì chúng ta thường áp dụng 4 quy tắc sau:
Quy tắc bỏ hằng số: VD: bạn tính ra TM của một function là 2n + 3n² + 10000 thì bỏ hết những hằng số (mấy số nằm dưới): 2, 3, 10000 → và nó trở thành n + n² Ps: Giá trị số hầu như không ảnh hưởng quá nhiều tới tốc độ thực thi chương trình
Quy tắc lấy Max: Cũng VD trên sau khi đã ra n + n² bạn tiếp tục lấy Max của phép toán → nó thành n²
Quy tắc cộng: Giống như việc cộng 2 funtions riêng biệt F(x) = n² và G(x) =m³ → TM cộng lại đc n² + m³
Quy tắc nhân: Quy tắc này giống như thực hiện 2 vòng for lồng nhau: n*m
Tham khảo các bài toán phổ biến và độ phức tạp của nó
Ta có bảng tham khảo nổi tiếng sau đây:
Độ phức tạp của một số thuật toán thường dùng
6. Túm lại như sau
Thật khó cho chúng ta do chưa có cơ hội đi làm và dấn thân vào dự án thực tế để có thể biết được tầm quan trọng của việc xác định độ phức tạp của thuật toán.Trước đây bản thân mình cứ nghĩ rằng miễn code chạy ngon là được, tuy nhiên cái mình chạy là màn hình console khi mà số dòng code chỉ là mấy chục và dữ liệu thì đơn giản. Sau vài năm nghe lỏm và học hỏi thì khi đi làm chúng ta làm việc với hệ thống cả nghìn khách hàng với dữ liệu phức tạp vô cùng nên đòi hỏi tối ưu từng dòng code để đạt được độ phức tạp tốt nhất có thể.
Ví dụ ta cần một thuật toán sắp xếp danh sách khách hàng để khi tìm kiếm thì chỉ cần nhấp chuột là ra kết quả. Khi đó cần nhắc thuật toán Sort nào nên dùng và Search như thể nào để giảm độ phức tạp nhất có thể lại vô cùng quan trọng va quyết định thành công của dự án rất nhiều.
PEACE !











Comments