JAVA - Tập 4: Data Structures và Algorithms

Sau hơn một tháng trời bị cuộc sống vùi dập, hôm nay mình xin tiếp tục viết tiếp về phần cấu trúc dữ liệu và giải thuật còn dang dở.

Nói sơ qua một chút ở bài viết số 3 thì mình đang còn dừng dở ở phần mã giả cho thuật toán Binary Search. Do đó hôm nay mình sẽ trình bày thêm một số hiểu biết về thuật toán này và đưa thêm một thuật toán sắp xếp mới là Bubble Sort để bàn luận.

Nội dung cụ thể như sau:

1. Thuật toán Binary Search (Tiếp)

2. Thuật toán Bubble Sort

Bắt đầu thôi nào !

1. Thuật toán Binary Search (Tiếp)

Độ phức tạp của thuật toán Binary Search là O(log2n). Có nghĩa là với mảng một chiều có n phần tử thì Binary Search yêu cầu tối đa là (1+log2n) so sánh, do đó so với thuật toán Linear Search thì giảm được rất nhiều so sánh và đạt được hiệu suất cao hơn trong đa số trường hợp tuy nhiên có một điều các bạn cần chú ý đó chính là đối với các mảng có số phần tử ít thì Binary Search không phát huy được hiệu suất khác biệt hơn so với các thuật toán khác nói chung hay Linear Search nói riêng.

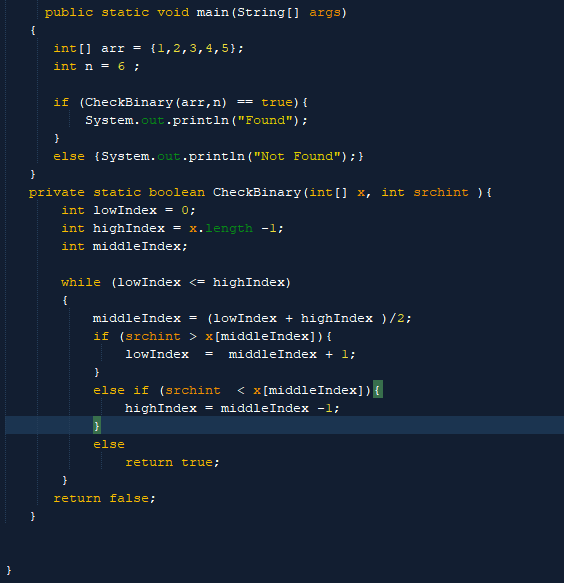
Đoạn code dưới đây thể hiện rõ được thuật toán Binary Search:

Phát hiện một con Bug trong thuật toán Binary Search:

Joshua Bloch (Tác giả của cuốn sách Effective Java) đã phát hiện ra một lỗi (Bug) trong quá trình nghiên cứu thuật toán Binary Search. Lỗi này trong Java khi thực thi thì sẽ thông báo là ArrayIndexOutOfBoundExeption. Lỗi này chỉ thể hiện khi số phần tử của mảng là 230 (Khoảng 1 tỷ) hoặc lớn hơn.

Rõ ràng khi mà bạn khai báo một biến integer thì nó không thể vượt qua 232 – 1 nên khi mà thực hiện phép toán midIndex = (loIndex + hiIndex) / 2; thì tổng của loIndex và hiIndex có thể vượt qua ngưỡng 232 – 1;

Để khắc phục lỗi này thì có một cách đó chính là thay thế phép toán midIndex = (loIndex + hiIndex) / 2; bằng phép toán sau:

midIndex = lowIndex + (loIndex - hiIndex) / 2;

Fun Fact:

Mặc dù Binary Search ra đời từ năm 1946 nhưng mãi đến năm 1962 thì nó mới được áp dụng vào chạy thực nghiệm lần đầu tiên.

OK, vậy là mình đã trình bày xong 2 thuật toán tìm kiếm đơn giản và dễ học xong. Sau đây mình sẽ tiếp tục trình bày các thuật toán về sắp xếp bao gồm Bubble Sort, Selection Sort và Insertion Sort.

2. Thuật toán Bubble Sort

Từ cái tên bạn cũng có thể hình dung một chút ít phần nào về thuật toán này rồi. Khi cơ chế của nó được hình dung thông qua các bọt bóng nổi lên trên mặt nước.

Sẽ có 2 vòng For chạy từ đầu mảng tới cuối mảng và ngược lại. Trong đó vòng for chạy từ cuối mảng là vòng for được lồng vào bên trong vòng for chạy từ đầu mảng. Khi mà 2 vòng for lồng với nhau như vậy thì có nghĩa là với mỗi lần duyệt qua giá trị của biến chạy vòng for mẹ thì nó sẽ duyệt hết toàn bộ vòng for con. Khi mà xuất hiện phần tử có giá trị nhỏ hơn thì nó tiến hành đổi vị trí cho nhau.

Sau đây là mã giả của thuật toán:

 DECLARE INTEGER i, pass
 DECLARE INTEGER x[] = [ ... ]
 FOR pass = 0 TO LENGTH(x) - 2
  FOR i = LENGTH(x) - 1 DOWNTO pass + 1
  IF x[i] LT x[pass] THEN // switch to > for descending sort
  EXCHANGE x[i], x[pass]
  END IF
  NEXT i
 NEXT pass
 END
 

Ví dụ ta có mảng một chiều như sau:

[ 18, 16, 90, -3 ]

Thì các bước chạy được thể hiện như sau:

Pass 0 Pass 1 Pass 2
====== ====== ======
18 16 90 -3 -3 16 90 18 -3 16 90 18
^ ^ ^ ^ ^ ^
| | | | | |
------------- --------- -----
-3 16 90 18 -3 16 90 18 -3 16 18 90
^ ^ ^ ^ 
| | | |
--------- -----
-3 16 90 18 -3 16 90 18
^ ^
| |
-----
-3 16 90 18

Code thực thi đơn giản như sau :

static void sort(int[] x)
 {
       for (int pass = 0; pass < x.length - 1; pass++)
               for (int i = x.length - 1; i > pass; i--)
                   if (x[i] < x[pass])
                    {
                         int temp = x[i];
                         x[i] = x[pass];
                         x[pass] = temp;
                    }
 }

Bài viết hôm nay hơi ngắn so với quy định. Hi vọng các bạn có thể đọc và đưa ra nhận xét.

Suy cho cùng thì một bài viết nếu quá dài thì mình nghĩ các bạn cũng không muốn đọc nữa nên mình xin kết thúc tại đây.

PEACE !