JAVA - Tập 3 | Data Structures và Algorithms | Mảng Một Chiều - One-Dimensional Arrays

Nội dung bài viết:

Bắt đầu bài viết này với việc tìm hiểu về mảng một chiều, các biến cho mảng một chiều, sau đó tiếp tục tìm hiểu 5 thuật toán tìm kiếm và sắp xếp mảng trong lập trình Java.

Mảng một chiều được xem là một công cụ để lưu trữ dữ liệu rất phổ biến trong kĩ thuật lập trình bằng việc xây dựng nên các Khối – Block để có thể lưu trữ những kiểu dữ liệu phức tạp. Hôm nay chúng ta sẽ tìm hiều Mảng một chiều được hiểu và sử dụng như thế nào trong lập trình Java. Đầu tiên sẽ là khởi đầu với các khái niệm liên quan đến Mảng một chiều sau đó là việc nó được biểu diễn như thế nào thông qua 3 cách thông thường được được sử dụng trong lập trình java. Cuối cùng ta tiếp tục tìm hiểu về 5 thuật toán được sử dụng để tìm kiếm và sắp xếp dành cho mảng một chiều như:

1. Linear Search

2. Binary Search

3. Buble Sort

4. Selection Sort

5. Insertion Sort

Trong bài viết trước đó ở series tự học Java này, mình đã có một bài viết giải thích Data Structure và Algorithm là gì rồi, nếu bạn chưa nắm rõ hay chưa đọc qua thì có thể tham khảo tại đây.

Nội dung bài viết hôm nay được chia làm 4 phần như sau:

· Định nghĩa thế nào là Mảng

· Mảng một chiều là gì ?

· Các biến trên Mảng

· Các thuật toán tìm kiếm và sắp xếp trên Mảng

I, Định nghĩa thế nào là Mảng

Mảng được hiểu nôm na là một chuỗi các elements và mỗi element thì được gắn liền với một số thứ tự của chính nó trong toàn bộ mảng đó.

Hiểu một cách sâu xa thì element chính là một tập hợp các vị trí bộ nhớ - memory locations, có nhiệm vụ lưu trữ một Data Item (Data Items thì có thể là Một số, một dữ liệu kiểu structure như Học Sinh, Công nhân ….). Nhắc lại là mỗi element thì được gắn với một chỉ số Index có nhiệm vụ xác định vị trí của một element nằm trong mảng, và rõ ràng là Index thì hiển nhiên là một số không âm.

Java hỗ trợ việc sử dụng array, mỗi element thì được phân phát một lượng bộ nhớ để lưu trữ dữ liệu là như nhau. Con số chính xác thì phụ thuộc vào Data item của mảng đó, và kiểu dữ liệu cho các Data item trên mảng bắt buộc phải giống nhau.

Chú ý quan trọng:

Trong Java, sau khi khởi tạo mảng thì không ai có thể điều chỉnh hay thay đổi kích thước của mảng đó được nữa. Nếu bạn muốn thay đổi kích thước của mảng thì bắt buộc phải khởi tạo lại một mảng khác với kích thước mảng momg muốn và coppy lại các element sang mảng mới khởi tạo này.

II, Mảng một chiều

Mảng một chiều được xem là kiểu mảng đơn giản và cơ bản nhất, được dùng để lưu một list các Data items. Mỗi element thì được gắn với duy nhất một chỉ số Index (So với mảng 2 chiều là 2: Hoành độ và Tung độ).

Đối với ngôn ngữ Java thì có tất cả có 3 cách để có thể khởi tạo một mảng một chiều:

· Sử dụng hình thức khởi tạo bình thường

· Sử dụng keyword New

· Kết hợp cả việc khởi tạo bình thường và từ khóa New

+ Khởi tạo một cách bình thường

Ví dụ:

{‘J’, ‘a’, ‘V’, ‘a’}

+ Tạo mảng với từ khóa New

Ví dụ

new char[4]

+ Kết hợp cả việc khởi tạo bình thường và từ khóa New

Ví dụ :

new char[] {‘J’, ‘a’, ‘V’, ‘a’}

III, Các biến trên mảng một chiều

Chúng ta có thể định nghĩa kiểu dữ liệu cho mảng hoặc cả số lượng phần tử của mảng một chiều đó.

Có 3 ví dụ như sau

 char[] name1 = { 'J', 'a', 'v', 'a' };
 char[] name2 = new char[4];
 char[] name3 = new char[] { 'J', 'a', 'v', 'a' };
 output(new char[] { 2, 3 }); // output({ 2, 3 }); results in a compiler error
 static void output(char[] name)
 {
  // ...
 }

Trong đoạn code trên thì name1 , name2, name3 được xem như là tên của mảng một chiều đó. Kiểu dữ liệu cho mảng đó chính là kiểu Char. Việc sử dụng từ khóa Char nhằm mục đích bắt buộc các elements chỉ được phép lưu trữ các giá trị có kiểu dữ liệu là Char.

Tuy nhiên trong một số trường hợp thì Java sẽ chuyển đổi kiểu dữ liệu sao cho phù hợp trong mảng.

Ví dụ dưới đây chương trình vẫn có thể thực thì do java chuyển kiểu int sang kiểu char được (Điều kiện là vẫn nằm trong khoảng dữ liệu đó, cụ thể kiểu char thì có thể chuyển các số nguyên kiểu int từ khoảng 0 – 65535, ngoài khoảng đó là bị lỗi).

char[] chars = { 'A', 10 };// Thực thi được !
char[] chars = { 'A', 80000 }; // Không thực thi được

Để lấy độ dài của mảng một chiều đó thì sử dụng thuộc tính .length

Ví dụ:

 name1.length // return 4

IV, Các thuật toán tìm kiếm và sắp xếp trên Mảng.

Tìm kiếm trên một Mảng để xác định được một Data Item hay nói cách khác là một giá trị trên Mảng thì chúng ta có khá nhiều thuật toán để có thể làm được điều đó. Một trong những thuật toán phổ biến đó chính là Linear Search hay là một thuật toán khác đó hiệu suất cao hơn nhưng đòi hỏi cao hơn khi để sử dụng Binary Search thì cần một Mảng đã được sắp xếp theo thứ tự (Tăng dần hoặc giảm dần). Nói đến thuật toán sắp xếp thì chúng ta có một số thuật toán sắp xếp phổ biến và cơ bản như Bubble Sort, Selection Sort, Insertion Sort, tuy không có hiệu suất quá cao đối với các mảng có số phần tử quá dài nhưng lại hoạt động tốt đối với những mảng một chiều ngắn.

+ Thuật toán Linear Search

Chúng ta cũng xem xét mã giả của thuật toán này như sau:

DECLARE INTEGER i, srch = ...
DECLARE INTEGER x[] = [ ... ]
FOR i = 0 TO LENGTH(x) - 1
 IF x[i] EQ srch THEN
 PRINT "Found ", srch
 END
 END IF
NEXT i
PRINT "Not found", srch
END

Hiểu nôm na thì ban đầu chúng ta sẽ có một giá trị cần tìm kiếm (Kiểu int hoặc char chẳng hạn) và một biến i với mục đích làm biến chạy.

Khi đó biến i đóng vai trò là biến chạy qua hết tất cả các elements của Array (Index). Ở mỗi vị trí index i thì thuật toán kiếm tra arr[i] có bằng giá trị cần tìm kiếm không. Nếu bằng thì xuất ra dòng “Found ” + Giá trị đó. Còn nếu duyệt toàn mảng mà không có thì xuất ra dòng “Not Found” + Giá trị cần tìm kiếm.

Độ phức tạp của Linear Search là O(n) do khi gặp trường hợp xấu nhất thì nó phải duyệt hết tất cả số phần tử của Mảng thì mới có thể tìm thấy giá trị cần tìm kiếm. Trung bình theo các nghiên cứu, nếu không gặp phải trường hợp xấu nhất thì chỉ cần trung bình n/2 so sánh thì thuật toán Linear Search có thể xác định được giá trị cần tìm.

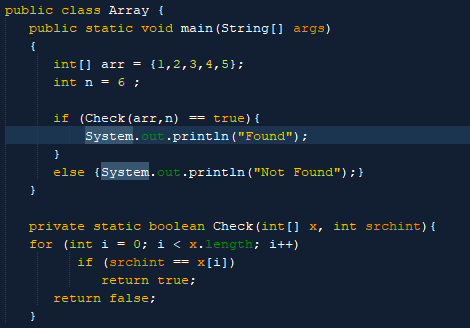
Xét đoạn code sau đây:

Đoạn code trên chính là hình dung đây đủ nhất của cơ chế làm việc của thuật toán Linear Search

+ Thuật toán Binary Search

Điều kiện để chạy thuật toán này đó chính là mảng của bạn phải được sắp xếp theo một thứ tự trước đó sẵn. (Mặc định là từ bé đến lớn)

Thuật toán được tuân theo các bước sau:

1. Cài đặt 2 chỉ số index là Low index và High index trong đó Low index chính là Data item đầu tiên của mảng, High index chính là Data item cuối cùng cùng của mảng.

2. Điều kiện để kết thúc thuật toán chính tìm đuọc giá trị cần kiếm hoặc là khi Low index lớn hơn High index, nếu việc đó xảy ra chứng tỏ không thể tìm thấy Data item đó trong mảng này.

3. So sánh giá trị cần tìm kiếm với giá trị Data item tại Middle index (bằng tổng Low index và High index sau đó chia 2 ). Nếu giống nhau thì kết thúc thuật toán.

4. Nếu giá trị cần tìm kiếm lớn hơn giá trị của Data item ở vị trí Middle index thì thay đổi giá trị Low index = Middle index + 1, sau đó quay trở lại bước 2, tính lại Middle index và so sánh tiếp. Việc tìm giá trị sẽ được diễn ra ở một nữa mảng bên phải.

5. Nếu giá trị cần tìm kiếm nhỏ hơn giá trị của Data item ở vị trí Middle index thì thay đổi giá trị High index = Middle index 1 1, sau đó quay trở lại bước 2, tính lại Middle index và so sánh tiếp. Việc tìm giá trị sẽ được diễn ra ở một nữa mảng bên trái.

Sau đây là mã giả của thuật toán:

 DECLARE INTEGER x[] = [ ... ]
 DECLARE INTEGER loIndex = 0
 DECLARE INTEGER hiIndex = LENGTH(x) - 1
 DECLARE INTEGER midIndex, srch = ...
 WHILE loIndex LE hiIndex
  midIndex = (loIndex + hiIndex) / 2
  IF srch GT x[midIndex] THEN
  loIndex = midIndex + 1
  ELSE
  IF srch LT x[midIndex] THEN
   hiIndex = midIndex - 1
  ELSE
  EXIT WHILE
  END IF
 END WHILE
 IF loIndex GT hiIndex THEN
  PRINT srch, " not found"
 ELSE
  PRINT srch, " found"
 END IF
 END
 

Về cơ bản thì mình thấy thuật toán này không khó để hiểu nhưng lại đạt được hiệu suất cao hơn so với thuật toán Linear Search.

Ở bài viết tiếp theo mình sẽ nói về các thuật toán sắp xế, hi vọng có ai đó có thể đọc được nạ.

PEACE